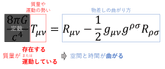【エッセイ・宇宙を泳ぐひと】第5回　ガウスびっくり、僕らぐんにゃり

1905年、スイス特許庁で働いていた無名の青年が突如として３つの論文を立て続けに発表した。その論文にはそれぞれ、当時の物理学界に革命を起こす画期的な理論が記されていた。量子力学の発展のきっかけとなった「光量子仮説」、統計物理学の基礎となった「ブラウン運動の理論」、そして特に斬新であった「相対性理論」は、当時大学側から博士論文としての受け入れを拒否されたほど革命的であったという。この衝撃的な出来事が起きた1905年は「奇跡の年」と呼ばれ、いまや伝説となっている。若きアインシュタイン、当時26歳のことである。ん……待て。当時26歳……？

おい、同い年やないか。

ああ、そうですか、この歳で……ね。うん、分かったよアインシュタインくん、君は天才だ。ベロでも何でも好きなだけ出していなさい。僕は僕で地道に研究を頑張るさ……。

相対性理論といえば、今や多くの人が「高速で動くと時間が遅れる」「光の速さは不変」「E=mc²」あたりの面白い話をちらっと聞いたことぐらいならあるだろう。ただそれらの話は相対性理論の中でも「特殊相対性理論」と呼ばれる限られた範囲の理論で説明されることがほとんどだ。「特殊」ではなく「一般相対性理論」の方が理論的には美しいので僕は好きなのだけれど、いかんせん使う数学がめちゃめちゃ難しいので、一般的にはなかなか説明されることが少ない。

とはいえ、僕の好きという気持ちが抑えられないので、ちょっとだけ一般相対性理論の重力場の方程式を見てみよう。
（※ どうしても数式を見ると吐き気と尿意が止まらなくなるという体質の方がいたら３段落飛ばして「まあ要するに、」でまたお会いしましょう。）

枠で囲んでいるものがこの式の主役だ。テ、テンソル……？リッチ……？富豪なの……？と早速われわれ庶民はお呼びでないオーラを放っているが、ざっくり理解しよう。

左辺の「エネルギー運動量テンソル」は、物体の質量と運動の勢いを表している。質量を表すものなのにエネルギーという名前が付いているのは、例のE=mc²という式を使えば「質量(m)はエネルギー(E)に置き換えられるのじゃ」とアインシュタインおじさんが言っているからだ。対して右辺の「計量」というものは時間と空間を合わせた４次元の長さを測る物差しのようなものだ。「リッチテンソル」の中身も実はこの計量だけで書き表せるので、右辺はすべて「物差しの長さの変化」についての式になっている。その他、Gとかcは全部定数なのであまり気にしなくいい。あと、上とか下についてるμとかνとかの文字も、式番号を表しているだけなのであまり気にしなくていい。ほうほう、なんとなく庶民にも分かる気がしてきたぞ。

しかし「なんだ、意外に簡単そうな式じゃん」と思った庶民は以下のリンクを見て反省してほしい。とある先人*1が例のリッチテンソルの中身を全て書き下した結果の式だ。ご覧あれ、見るもおぞましい数の計量たちの狂喜乱舞を。物差しの神に祟られたらこういう悪夢を見ると言い伝えられている。

http://anoda.web.fc2.com/oldpage/space/mlab07/gr.pdf

まあ要するに(おかえり)、このアインシュタインの重力方程式は、質量を持つ物体が存在していたりそいつが運動していたりすると（左辺）、それに応じて時間と空間の４次元世界の物差しが曲がりますよ（右辺）ということを数式的に表現しているのだ。アインシュタインは、物体は重力という力で進行方向を曲げられているのではなく、曲がった空間を真っすぐ進んでいるから曲がっているように見えるだけだと言っているのだ。例えば紙にまっすぐ直線を書いたとしても、その紙自体が曲がっていたら３次元世界の僕らから見れば曲がって見えるよね、というようなイメージだ。「高速で動くと時間が遅れる」という話も、「時間の物差しが曲がる」という意味でこの式に含まれている。

この世の中のあらゆるものは、ほんの少しずつではあるけれど周りの世界を曲げている。そいつが動くと、その運動によってさらに曲がりは大きくなる。かくいう僕らも、僕ら自身の質量や運動によってほんの少しだけ自分の周りの空間を曲げていて、しかもその曲がりによってさらに自分の運動が影響を受け、また曲がり方が変化する……という複雑なバランスの中に生きている。空間という固定された入れ物の中に僕らがポツンと存在しているのではなく、僕らの存在と周りの世界は常にお互いに影響されあいながら成り立っているのだ。なんだか空想のお話のように聞こえるけれど、確かに最先端の望遠鏡観測などによるとこのアインシュタインの理論は正しいらしい。

でも、言われてみれば確かに僕らの世界は曲がっているのかもしれない。人間が存在して、その人たちが集まって、ルールができて、ひとつの世界が生まれる時、その世界は既に曲がっている。歴史上の偉人が印刷された紙で商品を買える世界、関西に生まれたという理由だけで阪神タイガースの勝敗に一喜一憂する世界、エタノール入りの飲み物を一番多くイッキ飲みした人間が尊敬される世界、金曜ロードショーの特定の回にだけ異様に強い団結力で「バルス」とつぶやく世界、透明なビニールカーテンを間に挟んでTポイントカードのやり取りをする世界。傍から見ればなんだかねじ曲がったおかしな世界だ。

曲がっていること自体に良い/悪いということは多分ないんだろう。むしろ曲がっているからこそ、その曲がりを原動力として世界は前に進んでいる。そしてそれぞれに固有の曲がり方があるからこそ世界は面白くて、愛らしいようなところもある。

大学の演劇サークル時代のある事件を思い出す。その名も「ネコ事件」。

僕のいた劇団はやたらと規律が厳しいところで、役者たちは軍隊のようにリーダーの指示に従い、少しでも劇場のルールを破ると舞台監督にかめはめ波を撃たれ、集会に１秒でも遅刻すると劇団主宰が魔貫光殺砲をお見舞いするという恐ろしいサークルだった。

事件は、ある公演前の夜集会で起こった。劇団員全員が集まる大事な集会で、当然遅刻は厳禁。ピリリとした空気を感じながら全員がバタバタと席につく。そして点呼の時間。二年生のスタッフが１人いない。どうやら徹夜続きのため、作業部屋で仮眠を取っていたところを、誰も気づかずに置いてきてしまったらしい。ああ、やってしまった。

「１秒でも遅れると魔貫光殺砲」

全員の頭に恐ろしい戦場が浮かぶ。すぐさま彼と同じセクションのスタッフ（あだ名「ネコさん」）が立ち上がり、彼を起こしに走る。永遠のような沈黙。劇場にただならぬ空気が流れる。背筋を凍らせる一年生。表情を曇らせる二、三年生。そして僕は、ドキドキしていた。そう、当時劇団主宰をしていた僕が、魔貫光殺砲を放たなければいけなかったからだ。ああもう……説教とか苦手なのに。どうしよう。

ネコさんが戻ってきた。僕は覚悟を決め、劇団の威厳を保つべく臨戦態勢を取る。しかし、いない。遅刻した彼がいない。ネコさんが一人だけで戻ってきた。……ありゃ？

そしてネコさんは言う。

「すみません、起きませんでした。」

うん。

えーーーっと……ん、起きませんでした……？ってどういうこと……え……？起こすよね普通……？まさかこの状況で「そっと寝かせておく」という選択肢を選んだのかい……？

ざわつく劇場。ぐらつく視界。ぐんにゃりと世界が曲がる。え、死んでんの、と誰かがつぶやく。確かに、もはや死んでると考えた方がまだ納得がいく。言葉を失う二、三年生。息を止めて硬直する一年生。それでもなんとか劇団の威厳を保とうと真面目な顔をする僕。なぜか役目を果たした感を出して席に戻るネコさん。１か月間稽古してきた芝居よりよほど興味深いドラマ「ネコ事件」の爆誕である。

その後のことはあまり覚えていない。結局彼は死んでいなくて、僕はとりあえず威厳を損なわないための魔貫光殺砲を撃ってその場を流したような気がする。

きっとネコさんも、あまりの恐ろしい空気に頭が真っ白になり、冷静になればおかしすぎる「とりあえず一旦そっと寝かせておく」という選択肢を取ってしまったのだろう。でもそれはきっと、みんなを困らせようとしたわけでも、笑いを取ろうとしたわけでもない。彼女はきっと正しいことをしていると思っていた。真っすぐ進んでいると思っていた。その世界がぐんにゃぐにゃに曲がっているとは知らずに。みんなそうだった。傍から見ればコントみたいなあの状況で、本気で焦ったり青ざめたりしていたのだ。人が存在して、その人たちが何かに向かって突き進んでいる時、その質量と運動によって世界は曲がる。けれど、当の本人たちはまさか自分の世界が曲がっているなんて、思いもしていなかった。

自分が今いる世界が曲がっているかどうかを知ることはできるのだろうか？

これは実は数学的には面白い問いになる。例えば、地球が平面ではなく曲面だと知るには、海に行って水平線の曲がり方を見るとか、人工衛星から写真を撮るとかすればいい。そんな感じで、２次元の曲面を３次元の立場で俯瞰できるなら話は簡単なのだけど、アインシュタインが言っているのは僕らが生きている４次元の世界自体に曲がりがあるということだ。その曲がりを、５次元世界のような神の視点で俯瞰することなく知ることができるか？となるとなかなか難しい話になる。曲がっている世界の中にいる自分の物差しも曲がっているので、普通に生きていればまさか自分の世界が曲がっているだなんて思いもしないというわけだ。

この問いに対して、かの有名なガウスという天才おじさんは「世界の曲がり、頑張ればその世界の中にいる人からも認識できるやん！！」ということを数学的に証明した。曲がった世界の中に閉じ込められていても、注意深く長さや角度を測ればガウス曲率と呼ばれている曲がりの情報については得ることができるという定理だ。その名も「ガウスの驚異の定理」。なんだそのネーミング。その名の通り、ガウスおじさんが自分で発見して自分でびっくりした定理だから200年間こう呼ばれ続けている。「ガウスのビックリしちゃった定理」ということだ。「うわっ!ダマされた大賞」みたいでウケる。三四郎の小宮さんはあれだけドッキリに掛けられているのに１つも定理にならなくてかわいそう。

その世界の外に出なくても、注意深く自分のいる世界を観察すれば曲がり方を知ることができる。でもそれは簡単じゃない。僕が「ネコ事件」を笑い話にできるようになったのは、あの時の世界の曲がりをきちんと認識できるようになったのは、劇団を引退した後だったと思う。こうやって外から俯瞰してみれば簡単に分かるのだけれど、中にいる当時はそんなことを疑うことすらできなかった。そうやって訳も分からずなんかあたふたして、理不尽な魔貫光殺砲を撃ってしまったこともあった。

でもあの曲がりこそ、本当に愛すべきものだったんじゃないか。曲がっているからこそ、劇団は、人は、面白いんじゃないだろうか。その曲がりを僕がきちんと認識していれば、あの時もっと正しい言葉をかけることができたんじゃないか。そのことに気付けなかったことが、今になってじんわりと悔しい。

世界の曲がりを知るのは簡単なことじゃない。過去を振り返ってもそうだ。

世界は大きな亀に支えられていると思われていた時代があった。

地球が宇宙の中心だと思われていた時代があった。

竹槍でB29爆撃機を撃墜できると信じた時代があった。

工場廃水は海に流しても問題ないと思われていた時代があった。

部活中に水を飲むと根性が足りないと言われた時代があった。

どんな場所でも堂々とタバコを吸っていい時代があった。

教師が生徒に体罰をすることが当たり前だった時代があった。

彼らの後の時代を生きる僕らは、俯瞰的に当時の世界がいかに曲がっていたかを知ることができる。それを見て、「今の時代ではあり得ない」とか思ってしまう。でも、だからって当時の人が狂っていたなんて言うことはできないと思う。人間は、固定された「世界」や「時代」という入れ物の中にポツンと存在しているわけではない。人間の存在と周りの世界は常にお互いに影響されあいながら成り立っている。気づかないうちに、疑いもしないような「時代の当たり前」に沿って行動は曲げられてしまう。「自分がしっかりと芯のある人間なら、そんな馬鹿なことはしない」なんて思うのはきっと傲りだ。その「芯」だって世界とぐんにゃぐにゃに絡み合って成り立っているものなのだから。

今、僕らの生きている世界はどうなんだろう。

お金を払えばUber Eatsがやってくる。

トイレではトイレットペーパーでお尻を拭く。

おみくじに「大吉」と印字されていると運が良いという意味である。

結婚したら夫婦どちらかが苗字を失う。

エアコンは28度に設定していると環境にやさしい。

脂がのっていない牛の価値は低い。

女性を「ちゃん付け」で呼んでも仕事をクビにならない。

おじさんは化粧をしない。

肌は白い方がいい。

蚊を殺しても罪に問われることはない。

有名人を匿名で誹謗中傷しても罪に問われることはない。

たとえその有名人が自殺しても罪に問われることはない。

人が集まった時点で、もう既に僕らは曲がった空間の真っ只中にいる。でも、気づけない。自分が曲がっているだなんて思いもしないまま、曲がった世界を突き進んでいる。そして、未来の自分たちから見れば「あり得ない」と思うことを自然にやってしまっているのかもしれない。でも、そのことを時代のせいにしてはいけないと思う。世界の構造と僕らの存在は決して切り離すことができない。僕らの行動を曲げるその世界の曲がりの原因だって、僕らにある。

たまにでいい、元気な時でいいけれど、たまには「この世界、曲がってね？」と疑って、世界の曲率を知ろうとする努力を怠ってはいけないな、と思う。曲がっていること自体に良い/悪いということは多分ない。だから、その世界を生きる僕らが良い/悪いを決めていかなければいけない。それは難しいことだ。難しいけれど、きっとやれるとガウスは言うに違いない。きっと、曲がりがあるからこそ世界は面白くて、愛らしいのだ。曲がった世界と格闘しながら、それでもうまく愛していく僕らを見て、ガウスはまたあの時のようにビックリしてくれるだろうか。

ガウスびっくり　僕らぐんにゃり
曲がった世界はアインシュタイン　そんな世界を愛したい
Yeah

そういえばアインシュタインの風貌ってどんな感じだったっけ？と思ってさっき「アインシュタイン」で画像検索してみたら、画像の８割ぐらいは吉本ブサイク芸人王者のあの方の写真になってしまっていた。今や世間でいうアインシュタインはあなたなのか、稲田さん……。アインシュタインのあの有名なベロを出した写真と並んで、微妙な笑みを浮かべる稲田さん。ベロ、稲田、ベロ、稲田、稲田、稲田、ベロ、稲田、稲田、稲田。特徴的な三日月形のあごがチャーミング。

んー、曲がってるなあ。面白いなあ。愛らしいなあ。

*1 マツド・サイエンティスト研究所『研究報告7　時間と空間のシミュレーション（中間報告）』より。