はじめに
科学ポータルサイト「BuzzScience」です。今回はUmeeTのノーベル賞Weekということでノーベル物理学賞について寄稿させていただくことになりました。みなさん、今年のノーベル物理学賞はどんな理由で、誰に授与されたかご存知でしょうか?
今年のノーベル物理学賞は「トポロジカル相転移と物質のトポロジカル相の理論的発見」という理由で、D. J. Thouless, F. D. M. Haldane, J. M. Kosterlitzの三名に決定しました。近年、物性分野では実験家による受賞が続いていたため、理論の研究室ではかなり話題になりました。この受賞に関する解説はすでにBuzzScienceの方で書いたので(解説記事はこちら)、今回は受賞研究で発見された「トポロジー」が重要になってくる物理現象にどのようなものがあるのかに主眼を置いて書いていこうと思います。
[広告]
励起におけるトポロジー
授賞理由にあるトポロジカルという言葉は数学のトポロジーという理論からきています。トポロジーというのは、簡単に説明すると、集合や空間というものを連続的に変形させたときに変わらない性質を調べたり、その変わらない量である不変量によって分類をおこなう分野です。特に、ホモトピー理論と呼ばれるものがあり、それを用いて物質における励起を分類することができます。このとき重要になってくるのが秩序という考え方です。
量子力学的な物質は、ハミルトニアンというものによって、その性質が記述されます。このハミルトニアンに対して何らかの対称操作、例えば回転や反転といった操作を加えたときに、ハミルトニアンがまったく変わらないときがあります。このとき、ハミルトニアンは対称性をもっていると言います。物質の性質を記述するハミルトニアンが対称性を持つにもかかわらず、物質がその対称性を持たないときがあり、その物質は自発的対称性の破れが起きていると言われ、何らかの秩序を持っていることになります。この自発的対称性の破れという言葉は2008年のYoichiro Nambuの受賞時に話題になりましたね。
先ほど、励起という言葉が出てきました。この励起という概念は、秩序状態からのずれとして理解できます。つまり、秩序のある状態から、秩序が乱れた状態(多少でよい)への変化が励起です。励起には様々なものがあって、無限小の小さな変化で生まれることのできるものもあれば、ある程度の大きな変化が必要なものもあります。実は、トポロジカルな励起というのは、大きな変化を必要とするものになっています。
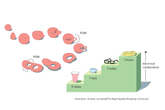
ここで具体的な例を考えてみましょう。最も身近な例としては磁石があります。磁石の性質を記述するハミルトニアンとして有名なものにHeisenbergハミルトニアンと呼ばれるものがあります。このHeisenbergハミルトニアンはSO(3)対称性、すなわち、三次元空間での回転に対する対称性を持っています。これを磁石の言葉で言うと、磁石を構成するたくさんの小さな磁石(スピン)が上下左右さまざまな方向を向いており、全体としてどちらを向いているということが言えない状態です。しかし、現実にはある方向を向いているため、大きな磁石としての性質を持っているわけです。よって、磁石はその性質を記述するハミルトニアンの対称性を持っていないため、自発的対称性が破れて、磁化という秩序をもった物質であるということができます。
次に、特殊な磁石を考えてみましょう。二次元上、すなわち、薄膜でできた磁石を考えます。先ほど述べた通り、磁石というのは、小さな磁石であるスピンが同じ方向を向くことでその性質を発現しています。二次元であってもそれは変わりません(正確に言えば、二次元のときは理論的に向きを揃えることができません)。さらに、今回は小さな磁石が二次元平面方向しか向けない場合を考えましょう。ちょうど時計の針のような感じです。このとき、真っ先に思いつく励起は、すべての小さな磁石をほんの少しずつだけ違う方向を向かせることです。この励起はスピン波と言われ、無限小のエネルギーで作ることができます。しかし、この励起はトポロジカルな励起ではありません。なぜなら、全部が同じ方向を向いた状態と少しずつ違う方向を向いた状態はトポロジー的には同じだからです。
では、どのような励起がトポロジカル励起になるのでしょうか?ここで考えている例の場合には、小さな磁石が渦を一つ作るようなときです。このような状態は、すべての小さな磁石が一つの方向を向いた状態とはトポロジー的に異なった状態となっています。このとき、隣りあう磁石はほとんど同じ方向を向くので無理な変形はしていないのですが、その渦を消そうと思うとどこかで無理やり向きを変えないといけないことがわかると思います。
このようにトポロジカルな励起は、作るのにも消すのにも大きなエネルギーが必要であることが知られています。実は、この性質は利点でもあるのです。トポロジーが同じ状態への変化にはほとんどエネルギーを必要としませんが、それはトポロジカルでない励起が壊れやすいことを意味しています。秩序が完全にある状態というのは情報量を持っていないので、量子計算などの技術に応用しようと思ったら励起状態を利用することになります。ところが、その励起状態が壊れてしまったら誤った結果を出力することになります。そこで、トポロジカルな励起を利用することによって、壊れにくい、安定なプロセスを実現できるのではないか、ということが期待されています。
量子ホール効果
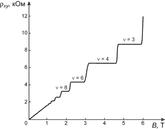
物質中でのトポロジーが巨視的に顔を出す顕著な例として量子ホール効果が知られています。この効果は、二次元平面中に閉じ込めた電子の集団を低温に冷やし強磁場をかけることで、ホール抵抗の値がh/e2 ≒25.81280745 kΩを整数で割ったものになる、というものです。1980年にvon Klitzingらによって実験的に発見され、1985年にその発見に対してノーベル物理学賞が与えられています。eは電子の電荷、hはプランク定数であり物理学の基本定数ですから、用いる物質や試料の形状に依存せず、多少の不純物が混入した程度では値が変わらない、という著しい性質を表しています。ホール抵抗はy方向に電圧Vyをかけ、x方向の電流Ixを図った時のVy/Ixで表されるので、測定は(低温、強磁場であることを除けば)簡単です。このようにシンプルな測定で、10桁もの精度で普遍的な値の抵抗値が現れる、ということで、現在では電気抵抗値の国際標準として用いられています。また、この現象はプランク定数が現れることから分かる通り量子力学的な現象なのですが、巨視的な電流の測定によって量子力学の帰結を見ることができるのも面白いですね。
実はここで現れた整数は物質中のトポロジカルな性質を反映した整数である、ということを今回の受賞者の一人であるThoulessと日本の甲元、Nightingale、Nijsらが1982年から1985年にかけて理論的に突き止め、今回の受賞理由となりました。ここで現れるトポロジーとは、波数空間で電子の波動関数が何回捻じれているかを表す整数であり、今日では発見者の四人の名前をとってTKNN数と呼ばれています。詳細な説明は難しいので省きますが、先ほど紹介した「トポロジカルな状態を壊すには大きなエネルギーが必要」という性質から、以下のように理解することができます。ホール抵抗の値がh/e2~25.8 kΩとなっている量子ホール状態を、ホール抵抗がh/e2÷2~12.9 kΩの状態へと遷移させようと、わずかなエネルギーを系に加えたとしましょう。この時、わずかなエネルギーでは25.8 kΩを25.7 kΩや25.9 kΩ には変化できても、一気に12.9 kΩへとジャンプさせることはできません。すなわち、量子ホール効果を示す状態はわずかなエネルギーでは壊せない、というトポロジカルな状態が示す性質を有しているのです。このように、量子ホール効果においては電流の大きさを外乱によって簡単には変えることができません。これはすなわちエネルギー損失のない電流を流せるということですから、超伝導と同様に省エネルギーなデバイスへの応用ができるのではないかと期待されているのです。
量子ホール効果の発見と解明ののち、受賞者の一人であるHaldaneは磁場なしでも量子ホール効果が起こる、いわゆる量子異常ホール効果の理論モデルを1988年に提唱しました。後にHaldane模型と呼ばれることになるこの模型は一見理論家の空想のようでしたが、2013年に中国のグループによって実験的にも観測がなされています。また、この先見的な模型を拡張したKane-Mele模型によって予言されたトポロジカル絶縁体は、後に実験的にも発見され、次世代の省エネルギーデバイス材料として期待を集めています。
このように量子ホール効果に関する研究に端を発し、ここで紹介したもの以外にも分数量子ホール効果、トポロジカル超伝導体、ワイル半金属など、電子の波動関数の持つトポロジーに由来する様々な現象や物質が発見され、今日では「トポロジカル物性」と呼ばれる一大分野として世界中で精力的な研究が行われています。
[広告]
おわりに
今回はトポロジーというものが現実の物質にどのように現れるのか、磁性体におけるトポロジカル励起と量子ホール効果を例に解説しました。他にも、トポロジーが重要になってくる物理現象は数多く発見されており、その応用も量子計算から身の回りのデバイスまで多岐にわたっています。
今回の受賞者たちは、そのようなトポロジカルな現象や状態を発見した先駆者たちでした。今回は彼らが発見したことについては直接的には触れなかったので、興味をもたれた方々は下記の記事なども読んでみてください。
BuzzScienceによる解説記事
http://buzzscience.net/archives/1916
学習院大学・田崎晴明教授による解説記事
http://webronza.asahi.com/science/articles/2016120100001
BUZZSCIENCEについて
科学ポータルサイトBuzzScienceは、最先端の科学を楽しく、面白く伝えることをモットーに研究解説記事を執筆しています。東京大学大学院統合物質科学リーダー養成プログラム(MERIT)に所属する博士課程学生有志からなる学生団体です。これからも継続的に活動を続けて参りますので、サイトにもお越しいただければ幸いです!
参考文献:Topological Phase Transitions and Topological Phases of Matter, ノーベル財団